3.6.7 Convert to Parametric

When a linear system has more than one solution, the solution set can be expressed as a tuple of equations, a vector of linear expressions or a linear surface (see §9.5.3). The tuple form is the result of linear conversion, described in §3.6.6 The vector and linear surface result from parametric conversion and participate in a cycle of transformations detailed in Figure 3.10

• If the subject is a linear system, it is transformed into a parametric vector. Internally, the subject is transformed to a matrix and reduced. Variable names in the subject are preserved through the internal transformations and reproduced in the result.
• If the subject is a matrix of scalars, it is transformed into a vector of expressions whose variables are the free variables of the system.
• If the subject is a parametric vector it is transformed to a linear surface.
• If the subject is a linear surface, it is transformed to parametric vector.
• Conversion of either parametric form back to matrix form is accomplished by →Linear .

Linear conversion can be used in conjunction with parametric conversion, matrix reduction and Solve to achieve a variety of transformations. A map of conversion transformations is given in Figure 3.11

3.6.7.1 Convert to parametric vector

When converting a matrix to a parametric vector, each column in the unaugmented portion contributes a component. Columns for which there is no pivot element contribute a free variable. Columns with a pivot element contribute a linear combination of the other columns with suitable negations.

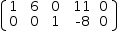
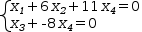
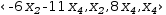
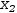
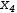
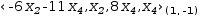
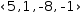
For example, the augmented matrix [(1, 6, 0, 11, 0), (0, 0, 1, -8, 0)] has pivot elements in columns 1 and 3, along with free variables in columns 2 and 4. The conversion proceeds as if producing the linear system (x_1+6⋅x_2+11⋅x_4=0, x_3+-8⋅x_4=0)ℓ but isolates the non-free variables. The result is a vector in which the non-free variables are expressed in terms of free variables: (-6⋅x_2-11⋅x_4, x_2, 8⋅x_4, x_4)ʋ. This expression has implied parameters x_2 and x_4. The vector can be evaluated at various points by supplying values for the parameters. Evaluation can be expression by an implied lambda expression. For example (λʋ(x_2, x_4)→(-6⋅x_2-11⋅x_4, x_2, 8⋅x_4, x_4)ʋ)(1, -1) implies (λʋ(x_2,x_4)→(-6⋅x_2-11⋅x_4,x_2,8⋅x_4,x_4)ʋ)(1,-1) and simplifies to (5, 1, -8, -1)ʋ.

3.6.7.2 Convert to linear surface

A linear surface (§9.5.3)is a slightly different parametric representation of a vector of linear expressions. It is essentially a tuple of vectors in which the first element is treated as a point and the subsequent elements are relative vectors, or attitudes. Points on the surface are generated by applying a continuum of scalar multiples to the attitudes. 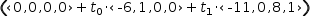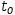For example, the previous example converts to the linear surface ((0, 0, 0, 0)ʋ, (-6, 1, 0, 0)ʋ, (-11, 0, 8, 1)ʋ) L where the parameters t_0 and t_1 are implied.

When converting a linear surface to a parametric vector, the augmented matrix is recovered from the subject and converted as described above.